JEE Physics Quiz for Wave on a String MCQ

For the wave shown in figure, the equation for the wave, travelling along +x axis with velocity 350 ms^–1 when its position at t = 0 is as shown

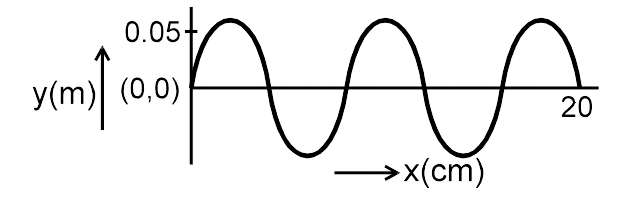
1. 0.05 sin (314/4 x –27475 t)
2. 0.05 sin (379/5 x –27475 t)
3. 1 sin (314/4 x –27475 t)
4. 0.05 sin (289/5 x +27475 t)

The displacement of a wave disturbance propagating in the positive x-direction is given by y = 1/(1 + x²) at time t = 0 and y = 1/[1 + (x – 1)²] at t = 2 seconds where x and y are in meters. The shape of the wave disturbance does not change during the propagation. The velocity of the wave is:

1. 2.5 m/s
2. 0.25 m/s
3. 0.5 m/s
4. 5 m/s

A transverse wave is described by the equation Y = Y₀ sin 2π (ft – x/λ). The maximum particle velocity is equal to four times the wave velocity if

1. λ = πY₀/4
2. λ = πY₀/2
3. λ = πY₀
4. λ = 2πY₀

A travelling wave on a string is given by y = A sin [αx + βt + π/6]. If α = 0.56 /cm, β = 12/sec, A = 7.5 cm, then position and velocity of particle at x = 1 cm and t = 1s is

1. 4.6 cm, 46.5 cm s^-1
2. 3.75 cm, 77.94 cm s^-1
3. 1.76 cm, 7.5 cm s^-1
4. 7.5 cm, 75 cm s^-1

A transverse wave of amplitude 0.50m, wavelength 1m and frequency 2 Hz is propagating on a string in the negative x-direction. The expression of the wave is

1. y(x, t) = 0.5 sin (2πx – 4πt)
2. y(x, t) = 0.5 cos (2πx + 4πt)
3. y(x, t) = 0.5 sin (πx – 2πt)
4. y(x, t) = 0.5 cos (2πx – 2πt)

Two small boats are 10m apart on a lake. Each pops up and down with a period of 4.0 seconds due to wave motion on the surface of water. When one boat is at its highest point, the other boat is at its lowest point. Both boats are always within a single cycle of the waves. The speed of the waves is

1. 2.5 m/s
2. 5.0 m/s
3. 14 m/s
4. 40 m/s

A wave pulse is generated in a string that lies along x-axis. At the points A and B, as shown in figure, if R_A and R_B are ratio of wave speed to the particle speed respectively then:

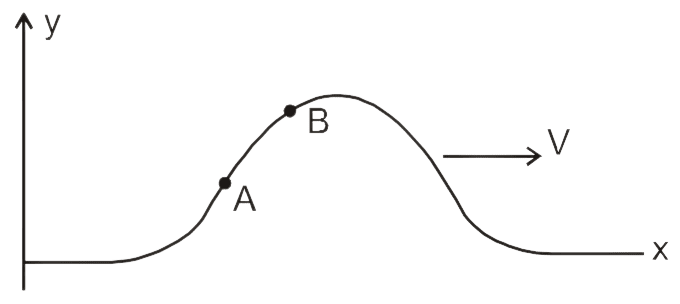
1. R_A > R_B
2. R_B > R_A
3. R_A = R_B
4. Information is not sufficient to decide.

Wave pulse on a string shown in figure is moving to the right without changing shape. Consider two particles at positions x₁ = 1.5 m and x₂ = 2.5 m. Their transverse velocities at the moment shown in figure are along directions:

1. positive y–axis and positive y–axis respectively
2. negative y–axis and positive y–axis respectively
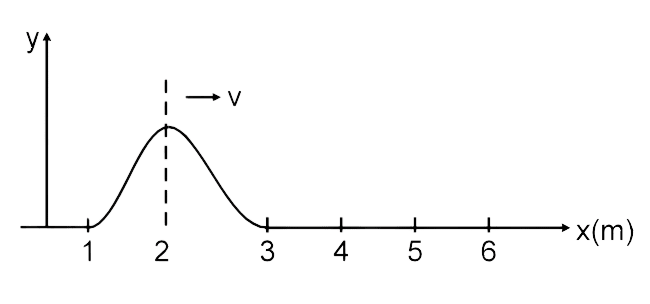
3. positive y–axis and negative y–axis respectively
4. negative y–axis and negative y–axis respectively

An observer standing at the sea-coast observes 54 waves reaching the coast per minute. If the wavelength of wave is 10m, The velocity of wave is

1. 19 m/sec
2. 29 m/sec
3. 9 m/sec
4. 39 m/sec

Both the strings, shown in figure, are made of same material and have same cross-section. The pulleys are light. The wave speed of a transverse wave in the string AB is v₁ and in CD it is v₂. The v₁/v₂ is

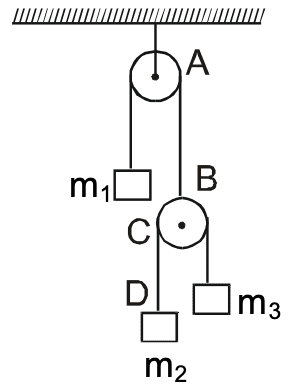
1. 1
2. 2
3. √2
4. 1/√2

Three blocks I, II, & III having mass of 1.6 kg, 1.6 kg and 3.2 kg respectively are connected as shown in the figure. The linear mass density of the wire AB, CD and DE are 10 g/m, 8 g/m and 10 g/m respectively. The speed of a transverse wave pulse produced in AB, CD and DE are : (g = 10 m/sec²)

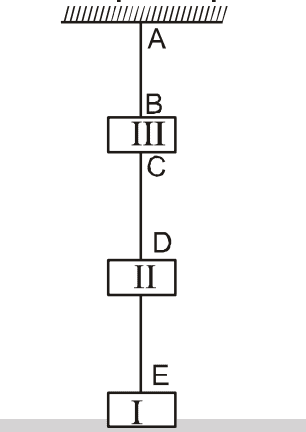
1. 80 m/s, 20√10 m/s, 40 m/s
2. 20√10 m/s, 40 m/s, 80 m/s
3. 20√10 m/s in all
4. 80 m/s in all

Three consecutive flash photographs of a travelling wave on a string are reproduced in the figure here. The following observations are made. Mark the one which is correct. (Mass per unit length of the string = 3 g/cm.)

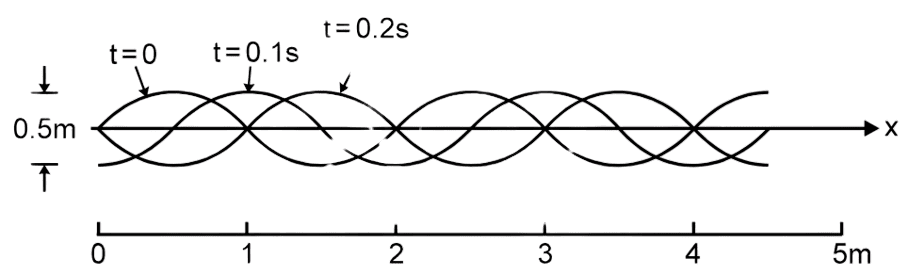
1. displacement amplitude of the wave is 0.25 m, wavelength is 1 m, wave speed is 2.5 m/s and the frequency of the driving force is 0.2/s.
2. displacement amplitude of the wave is 2.0 m, wavelength is 2 m, wave speed is 0.4 m/s and the frequency of the driving force is 0.7/s.
3. displacement amplitude of the wave is 0.25 m, wavelength is 2 m, wave speed is 5 m/s and the frequency of the driving force is 2.5 /s.
4. displacement amplitude of the wave is 0.5 m, wavelength is 2 m, wave speed is 2.5 m/s and the frequency of the driving force is 0.2/s.

A heavy ball is suspended from the ceiling of a motor car through a light string. A transverse pulse travels at a speed of 50 cm/s on the string when the car is at rest and 52 cm/s when the car accelerates on a horizontal road. Then acceleration of the car is : (Take g = 10 m/s²)

1. 2.7 m/s²
2. 3.7 m/s²
3. 2.4 m/s²
4. 4.1 m/s²

A wave moving with constant speed on a uniform string passes the point x = 0 with amplitude A₀, angular frequency ω₀ and average rate of energy transfer P₀. As the wave travels down the string it gradually loses energy and at the point x = l, the average rate of energy transfer becomes P₀/2. At the point x = l, angular frequency and amplitude are respectively :

1. ω₀ and A₀/√2
2. ω₀/√2 and A₀
3. less than ω₀ and A₀
4. ω₀/√2 and A₀/√2

A sinusoidal wave with amplitude y_m> is travelling with speed V on a string with linear density ρ. The angular frequency of the wave is ω. The following conclusions are drawn. Mark the one which is correct.

1. doubling the frequency doubles the rate at which energy is carried along the string
2. if the amplitude were doubled, the rate at which energy is carried would be halved
3. if the amplitude were doubled, the rate at which energy is carried would be doubled
4. the rate at which energy is carried is directly proportional to the velocity of the wave.

Sinusoidal waves 5.00 cm in amplitude are to be transmitted along a string having a linear mass density equal to 4.00 × 10^-2 kg/m. If the source can deliver a average power of 90 W and the string is under a tension of 100 N, then the frequency at which the source can operate is (take π² = 10):

1. 45 Hz
2. 50 Hz
3. 30 Hz
4. 62 Hz

The average power transmitted through a given point on a string supporting a sine wave is. 0.40 watt when the amplitude of wave is 2 mm. What average power will transmitted through this point its amplitude is increased to 4 mm.

1. 0.40 watt
2. 0.80 watt
3. 1.2 watt
4. 1.6 watt