JEE Physics Quiz Simple Harmonic Motion MCQ

According to a scientists, he applied a force F= –cx^1/3 on a particle and the particle is performing SHM. No other force acted on the particle. He refuses to tell whether c is a constant or not. Assume that he had worked only with positive x then :

1. as x increases c also increases
2. as x increases c decreases
3. as x increases c remains constant
4. the motion cannot be SHM

A particle performing SHM takes time equal to T (time period of SHM) in consecutive appearances at a particular point. This point is :

1. An extreme position
2. The mean position
3. Between positive extreme and mean position
4. Between negative extreme and mean position

A particle executing linear SHM. Its time period is equal to the smallest time interval in which particle acquires a particular velocity →v, the magnitude of →v may be :

1. Zero
2. V_max
3. V_max/2
4. V_max/√2

If →F is force vector, →v is velocity vector, →a vector is acceleration vector and →r vector is displacement vector with respect to mean position than which of the following quantities are always non-negative in a simple harmonic motion along a straight line?

1. →F.→a
2. →v.→r
3. →a.→r
4. →F.→r

Two SHM’s are represented by y = a sin (ωt – Φ) and y = b cos (ωt – Φ). The phase difference between the two is :

1. π/2
2. π/4
3. π/6
4. 3π/4

How long after the beginning of motion is the displacement of a harmonically oscillating particle equal to one half its amplitude if the period is 24s and particle starts from rest.

1. 12s
2. 2s
3. 4s
4. 6s

The magnitude of average acceleration in half time period from equilibrium position in a simple harmonic motion is

1. 2Aω²/π
2. Aω²/2π
3. Aω²/√2π
4. Zero

A particle performing SHM on the y axis according to equation y = A + B sinωt. Its amplitude is :

1. A
2. B
3. A + B
4. √A²+B²

Two particles execute S.H.M. of same amplitude and frequency along the same straight line from same mean position. They cross one another without collision, when going in opposite directions, each time their displacement from mean position is half of their amplitudes. The phase-difference between them is

1. 0°
2. 120°
3. 180°
4. 135°

A body executing SHM passes through its equilibrium. At this instant, it has

1. maximum potential energy
2. maximum kinetic energy
3. minimum kinetic energy
4. maximum acceleration

The K.E. and P.E of a particle executing SHM with amplitude A will be equal when its displacement is

1. √2A
2. A/2
3. A/√2
4. √2/3 A

A point particle of mass 0.1 kg is executing S.H.M. of amplitude of 0.1 m. When the particle passes through the mean position, its kinetic energy is 8 × 10^-3J. The equation of motion of this particle when the initial phase of oscillation is 45° can be given by

1. 0.1 cos(4t+π/4)
2. 0.1 sin(4t+π/4)
3. 0.4 sin(t+π/4)
4. 0.2 sin(π/2 + 2t)

For a particle performing SHM :

1. The kinetic energy is never equal to the potential energy
2. the kinetic energy is always equal to the potential energy
3. The average kinetic energy in one time period is equal to the average potential in this period
4. The average kinetic energy in any time interval is equal to average potential energy in that interval

Acceleration a versus time t graph of a body in SHM is given by a curve shown below. T is the time period. Then corresponding graph between kinetic energy KE and time t is correctly represented by

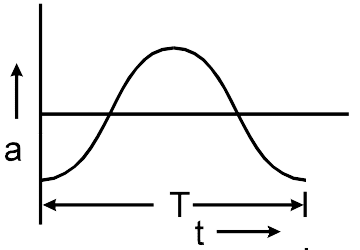
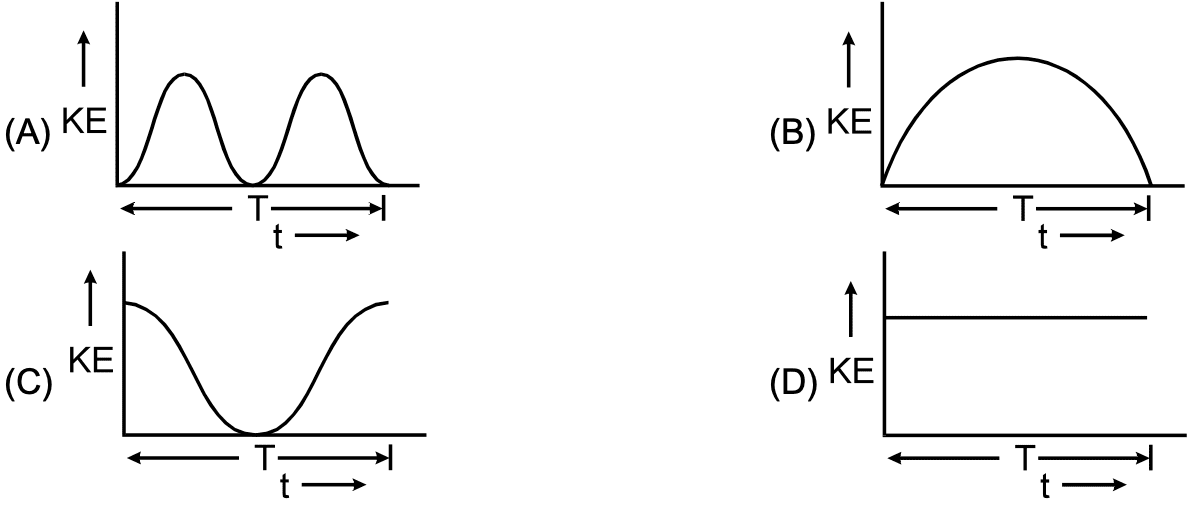
1. A
2. B
3. C
4. D

A particle performs S.H.M. of amplitude A along a straight line. When it is at a distance √3/2 A from mean position, its kinetic energy gets increased by an amount 1/2 m ω² A² due to an impulsive force. Then its new amplitude becomes:

1. √5 / 2 A
2. √3 / 2 A
3. √2 A
4. √5 A

Two spring mass systems have equal mass and spring constant k₁ and k₂. If the maximum velocities in two systems are equal then ratio of amplitude of 1st to that of 2nd is :

1. √k₁/k₂
2. k₁/k₂
3. k₂/k₁
4. √k₂/k₁

A toy car of mass m is having two similar rubber ribbons attached to it as shown in the figure. The force constant of each rubber ribbon is k and surface is frictionless. The car is displaced from mean position by x cm and released. At the mean position the ribbons are undeformed. Vibration period is

1. 2π√m(2k)/k²
2. 1/2π√m(2k)/k²
3. 2π√m/k
4. 2π√m/k+k

A mass of 1 kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :

1. 1 kg
2. 2 kg
3. 3 kg
4. 4 kg

A ball of mass m kg hangs from a spring of spring constant k. The ball oscillates with a period of T seconds. If the ball is removed, the spring is shortened (with respect to length in mean position) by

1. gT²/(2π)² metre
2. 3T²g/(2π)² metre
3. Tm/k metre
4. Tk/m metre

A smooth inclined plane having angle of inclination 30° with horizontal has a mass 2.5 kg held by a spring which is fixed at the upper end as shown in figure. If the mass is taken 2.5 cm up along the surface of the inclined plane, the tension in the spring reduces to zero. If the mass is then released, the angular frequency of oscillation in radian per second is

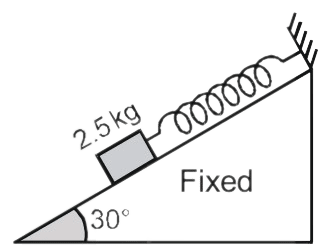
1. 0.707
2. 7.07
3. 1.414
4. 14.14

A particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part is used to continue the simple harmonic motion, the time period will

1. remain T
2. become 2T
3. become T/2
4. become T/√2

Four massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane (as shown in figure). If the mass M is displaced in the horizontal direction, then the frequency of the system.

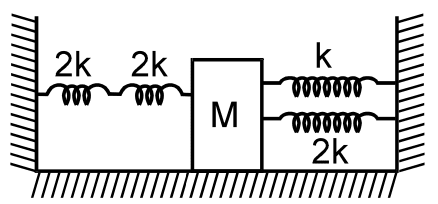
1. 1/2π √k/4M
2. 1/2π √4k/M
3. 1/2π √k/7M
4. 1/2π √7k/M

The total mechanical energy of a particle of mass m executing SHM with the help of a spring is E = (1/2)mω²A². If the particle is replaced by another particle of mass m/2 while the amplitude A remains same. New mechanical energy will be :

1. √2 E
2. 2E
3. E/2
4. E

Two pendulums begin to swing simultaneously. The first pendulum makes 9 full oscillations when the other makes 7. Find the ratio of length of the two pendulums.

1. 49/81
2. 7/9
3. 50/81
4. 1/2

Two pendulums at rest start swinging together. Their lengths are respectively 1.44 m and 1 m. They will again start swinging in same phase together after (of longer pendulum) :

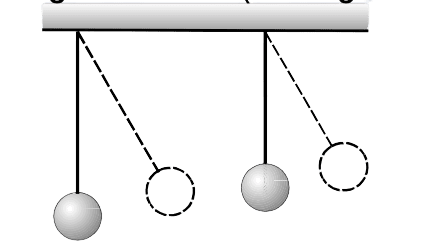
1. 1 vibration
2. 3 vibrations
3. 4 vibrations
4. 5 vibrations

A scientist measures the time period of a simple pendulum as T in a lift at rest. If the lift moves up with acceleration as one fourth of the acceleration of gravity, the new time period is

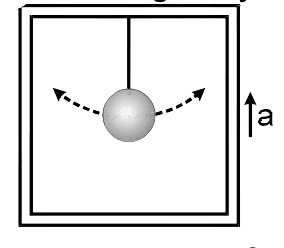
1. T/4
2. 4T
3. 2/√5 T
4. √5/2 T

A simple pendulum has some time period T. What will be the percentage change in its time period if its amplitude is decreased by 5%?

1. 6 %
2. 3 %
3. 1.5 %
4. 0 %

A simple pendulum with length l and bob of mass m executes SHM of small amplitude A. The maximum tension in the string will be

1. mg(1 + A/l)
2. mg(1 + A/l)²
3. mg[1 + (A/l)²]
4. 2 mg

A 25 kg uniform solid sphere with a 20 cm radius is suspended by a vertical wire such that the point of suspension is vertically above the centre of the sphere. A torque of 0.10 N-m is required to rotate the sphere through an angle of 1.0 rad and then the orientation is maintained. If the sphere is then released, its time period of the oscillation will be :

1. π second
2. √2π second
3. 2π second
4. 4π second

A metre stick swinging about its one end oscillates with frequency f₀. If the bottom half of the stick was cut off, then its new oscillation frequency will be :

1. f₀
2. √2f₀
3. 2f₀
4. 2√2f₀

When two mutually perpendicular simple harmonic motions of same frequency, amplitude and phase are superimposed

1. the resulting motion is uniform circular motion.
2. the resulting motion is a linear simple harmonic motion along a straight line inclined equally to the straight lines of motion of component ones.
3. the resulting motion is an elliptical motion, symmetrical about the lines of motion of the components.
4. the two S.H.M. will cancel each other.

The position of a particle in motion is given by y = Csinωt + Dcosωt w.r.t. origin. Then motion of the particle is:

1. SHM with amplitude C+D
2. SHM with amplitude √C²+D²
3. SHM with amplitude (C+D)/2
4. not SHM

A simple harmonic motion is given by y = 5 (sin 3πt + 3 cos √3πt). What is the amplitude of motion if y is in m ?

1. 100 cm
2. 5 m
3. 200 cm
4. 1000 cm

The position vector of a particle moving in x-y plane is given by r = (A sinωt)ˆi +(A cosωt) ˆj then motion of the particle is :

1. SHM
2. on a circle
3. on a straight line
4. with constant acceleration

When an oscillator completes 100 oscillations its ampliutde reduced to 1/3 of initial value. What will be its amplitude, when it completes 200 oscillations :

1. 1/8
2. 2/3
3. 1/6
4. 1/9

The damping force on an oscillator is directly proportional to the velocity. The units of the constant of proportionality are :

1. kgms^-1
2. kgms^-2
3. kgs^-1
4. kgs