JEE Physics Quiz Surface Tension MCQ

A thread is tied slightly loose to a wire frame as shown in the figure. And the frame is dipped into a soap solution and taken out. The frame is completely covered with the film. When the portion A is punctured with a pin, the thread :

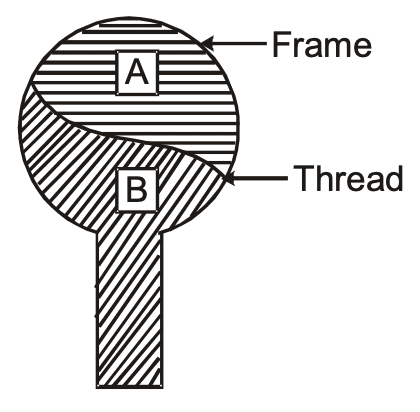
1. becomes convex towards A
2. becomes concave towards A
3. remains in the initial position
4. either (A) or (B) depending on size of A w.r.t. B

In a surface tension experiment with a capillary tube water rises upto 0.1 m. If the same experiment is repeated in an artificial satellite, which is revolving around the earth ; water will rise in the capillary tube upto a height of :

1. 0.1 m
2. 0.2 m
3. 0.98 m
4. full length of tube

A thin metal disc of radius r floats on water surface and bends the surface downwards along the perimeter making an angle θ with vertical edge of the disc. If the disc displaces a weight of water W and surface tension of water is T, then the weight of metal disc is :

1. 2πrT + W
2. 2πrT cosθ – W
3. 2πrT cosθ + W
4. W – 2πrT cosθ

The surface tension of a liquid is 5 Newton per metre. If a film is held on a ring of area 0.02 metres2, its surface energy is about :

1. 5 × 10^–2 J
2. 2.5 × 10^–2 J
3. 2 × 10^–1 J
4. 3 × 10^–1 J

The radii of the two columns is U-tube are r1 and r2. When a liquid of density ρ (angle of contact is 0°) is filled in it, the level difference of liquid in two arms is h. The surface tension of liquid is: (g = acceleration due to gravity) :

1. ρghr₁r₂/2(r₂ – r₁)
2. ρgh(r₂ – r₁)/2r₁r₂
3. 2(r₂ – r₁)/ρghr₁r₂
4. ρgh/2(r₂ – r₁)

Water rises in a capillary tube to a height h. it will rise to a height more than h

1. on the surface of sun
2. in a lift moving down with an acceleration
3. at the poles
4. in a lift moving up with an acceleration.

Insects are able to run on the surface of water because :

1. insects have less weight
2. insects swim on water
3. of the Archimede’s upthrust
4. surface tension makes the surface behave as elastic membrane.

A tube of fine bore AB is connected to a manometer M as shown. The stop cock S controls the flow of air. AB is dipped into a liquid whose surface tension is σ. On opening the stop cock for a while, a bubble is formed at B and the manometer level is recorded, showing a difference h in the levels in the two arms. if ρ be the density of manometer liquid and r the radius of curvature of the bubble, then the surface tension σ of the liquid is given by

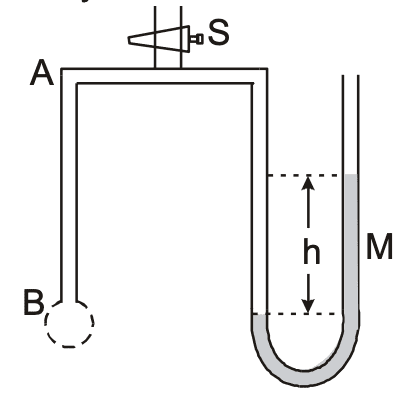
1. ρhrg
2. 2ρhrg
3. 4ρhrg
4. rhρg/4

Two parallel glass plates are dipped partly in the liquid of density ‘d’ keeping them vertical. If the distance between the plates is ‘x’, Surface tension for liquid is T & angle of contact is θ then rise of liquid between the plates due to capillary will be :

1. T cosθ/xd
2. 2T cosθ/xdg
3. 2T/xdgcosθ
4. T cosθ/xdg

When charge is given to a soap bubble, it shows :

1. a decrease in size
2. no change in size
3. an increase in size
4. sometimes an increase and sometimes a decreases in size

A water drop is divided into 8 equal droplets. The pressure difference between the inner and outer side of the big drop will be :

1. same as for smaller droplet
2. 1/2 of that for smaller droplet
3. 1/4 of that for smaller droplet
4. twice that for smaller droplet

An air bubble of radius r in water is at a depth h below the water surface at some instant. If P is atmospheric pressure, d and T are density and surface tension of water respectively, the pressure inside the bubble will be :

1. P + hdg – 4T/r
2. P + hdg + 2T/r
3. P + hdg – 2T/r
4. P + hdg + 4T/r

The work done to get n smaller equal size spherical drops from a bigger size spherical drop of water is proportional to :

1. (1/n^2/3)-1
2. (1/n^1/3)-1
3. n^1/3-1
4. n^4/3-1

Two unequal soap bubbles are formed one on each side of a tube closed in the middle by a tap. What happens when the tap is opened to put the two bubbles in communication ?

1. No air passes in any direction as the pressures are the same on two sides of the tap
2. Larger bubble shrinks and smaller bubble increases in size till they become equal in size
3. Smaller bubble gradually collapses and the bigger one increases in size
4. None of the above

A soap bubble in vacuum has a radius of 3 cm and another soap bubble in vacuum has a radius of 4 cm. If the two bubbles coalesce under isothermal conditions then the radius of the new bubble is :

1. 2.3 cm
2. 4.5 cm
3. 5 cm
4. 7 cm

A cylinder with a movable piston contains air under a pressure p₁ and a soap bubble of radius ‘r’. The pressure p₂ to which the air should be compressed by slowly pushing the piston into the cylinder for the soap bubble to reduce its size by half will be : (The surface tension is σ, and the temperature T is maintained constant)

1. [8p₁ + 24σ/r]
2. [4p₁ + 24σ/r]
3. [2p₁ + 24σ/r]
4. [2p₁ + 12σ/r]

A vessel whose bottom has round holes with a diameter of d = 0.1 mm is filled with water. The maximum height of the water level h at which the water does not flow out, will be : (The water does not wet the bottom of the vessel). [S.T of water = 70 dyn/cm]

1. h = 24.0 cm
2. h = 25.0 cm
3. h = 26.0 cm
4. h = 28.0 cm