JEE Maths Quiz Fundamentals of Mathematics-I MCQ

The set of intelligent students in a class is-

1. a null set
2. a singleton set
3. a finite set
4. not a well defined collection

The set A = {x : x ε R, x² = 16 and 2x = 6} is

1. Null set
2. Singleton set
3. Infinite set
4. not a well defined collection

If A = {x : –3 < x < 3, x ε Z} then the number of subsets of A is –

1. 120
2. 30
3. 31
4. 32

Which of the following are true ?

1. [3, 7] ⊂ (2, 10)
2. (0, ∞) ⊂ (4, ∞)
3. (5, 7] ⊂ [5, 7)
4. [2, 7] ⊂ (2.9, 8)

The number of subsets of the power set of set A = {7, 10, 11} is

1. 32
2. 16
3. 64
4. 256

Which of the folowing sets is an infinite set ?

1. Set of divisors of 24
2. Set of all real number which lie between 1 and 2
3. Set of all humman beings living in India.
4. Set of all three digit natural numbers

Let A = {x : x ε R, –1 < x < 1} , B={x : x ε R, x <=0 or x=> 2} and A ∪ B = R – D, then the set D is

1. {x : 1 < x <=2}
2. {x : 1 <= x < 2}
3. {x : 1 <= x <=2}
4. {x : 1 < x < 2}

If A = {2, 3, 4, 8, 10}, B = {3, 4, 5, 10, 12}, C = {4, 5, 6, 12, 14} then (A ∩ B) ∪ (A ∩ C) is equal to

1. {3, 4, 10}
2. {2, 8, 10}
3. {4, 5, 6}
4. {3, 5, 14}

The shaded region in the given figure is

1. A ∩ (B ∪ C)
2. A ∪ (B ∩ C)
3. A ∩ (B – C)
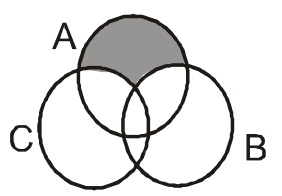
4. A – (B ∪ C)

Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 5}, B = {6, 7}, then A ∩ B’ is

1. B’
2. A
3. A’
4. B

If A = {x : x = 4n + 1, n <=> 5, n ε N} and B = {3n : n <=> 8, n ε N}, then A – (A – B) is :

1. {9, 21}
2. {9, 12}
3. {6, 12}
4. {6, 21}

A ∪ B = A ∩ B if :

1. A ⊂ B
2. A = B
3. A ⊃ B
4. A ⊄ B

Consider the following statements :

1. N ∪ (B ∩ Z) = (N ∪ B) ∩ Z for any subset B of R, where N is the set of positive integers, Z is the set of integers, R is the set of real numbers.
2. Let A = {n ε N : 1 <= n <=24, n is a multiple of 3}. There exists no subset B of N such that the number of elemets in A is equal to the number of elements in B.

Which of the above statements is/are correct ?

1. 1 only
2. 2 only
3. Both 1 and 2
4. Neither 1 nor 2

Which of the following venn-diagrams best represents the sets of females, mothers and doctors ?

1. A
2. B
3. C
4. D

Let A and B be two sets. Then

1. n(A ∪ B) <= n(A ∩ B)
2. n(A ∩ B) <=> n(A ∪ B)
3. n(A ∩ B) = n(A ∪ B)
4. can’t be say

In a city 20 percent of the population travels by car, 50 percent travels by bus and 10 percent travels by both car and bus. Then persons travelling by car or bus is

1. 80 percent
2. 40 percent
3. 60 percent
4. 70 percent

A class has 175 students. The following data shows the number of students obtaining one or more subjects : Mathematics 100, Physics 70, Chemistry 40, Mathematics and Physics 30, Mathematics and Chemistry 28, Physics and Chemistry 23, Mathematics & Physics & Chemistry 18. How many students have offered Mathematics alone ?

1. 35
2. 48
3. 60
4. 22

31 candidates appeared for an examination, 15 candidates passed in English, 15 candidates passed in Hindi, 20 candidates passed in Sanskrit. 3 candidates passed only in English. 4. candidates passed only in Hindi, 7 candidates passed only in Sanskrit. 2 candidates passed in all the three subjects How many candidates passed only in two subjects ?

1. 17
2. 15
3. 22
4. 14